If you’ve ever wondered how researchers make sure their samples accurately represent diverse populations, the answer lies in stratified random sampling. Unlike simple random sampling, which treats the entire population as a single, homogenous group, stratified random sampling dives deeper. It separates the population into meaningful subgroups, or strata, to ensure every slice of the population gets its say. Let’s take a closer look at what stratified random sampling is, how it works, and why it’s an essential tool in research and marketing.
What is Stratified Random Sampling?
Stratified random sampling is a probability sampling method that divides a population into smaller, defined subgroups, or strata, based on shared characteristics—such as age, income, or gender. Once the population is divided into these distinct strata, a random sample is drawn from each subgroup.
This technique ensures that each subgroup is properly represented in the final sample. Imagine you’re surveying people about their voting habits, and you divide the population into different age brackets. By random sampling within each age group, you’re ensuring that every generation has representation in your results. It’s a method designed to reduce bias and make your findings more accurate and reflective of the larger population.
Types of Stratified Random Sampling
1. Proportionate Stratified Random Sampling
In proportionate sampling, each stratum's sample size is proportional to its population size relative to the overall population. This method ensures that larger strata have a larger sample size, while smaller strata have fewer participants.

Example
Each sample size is proportional to the population size of the strata.
2. Disproportionate Stratified Random Sampling
In disproportionate sampling, the sample size for each stratum is not directly proportional to its population size. Instead, different sampling fractions are used for different strata. This approach is often employed when some strata are of greater interest or importance to the research.
Example
In this case, each stratum has a different sampling fraction, leading to varying sample sizes.
Process: How to do Stratified Random Sampling
Executing stratified random sampling requires a systematic approach. Below is a step-by-step guide:
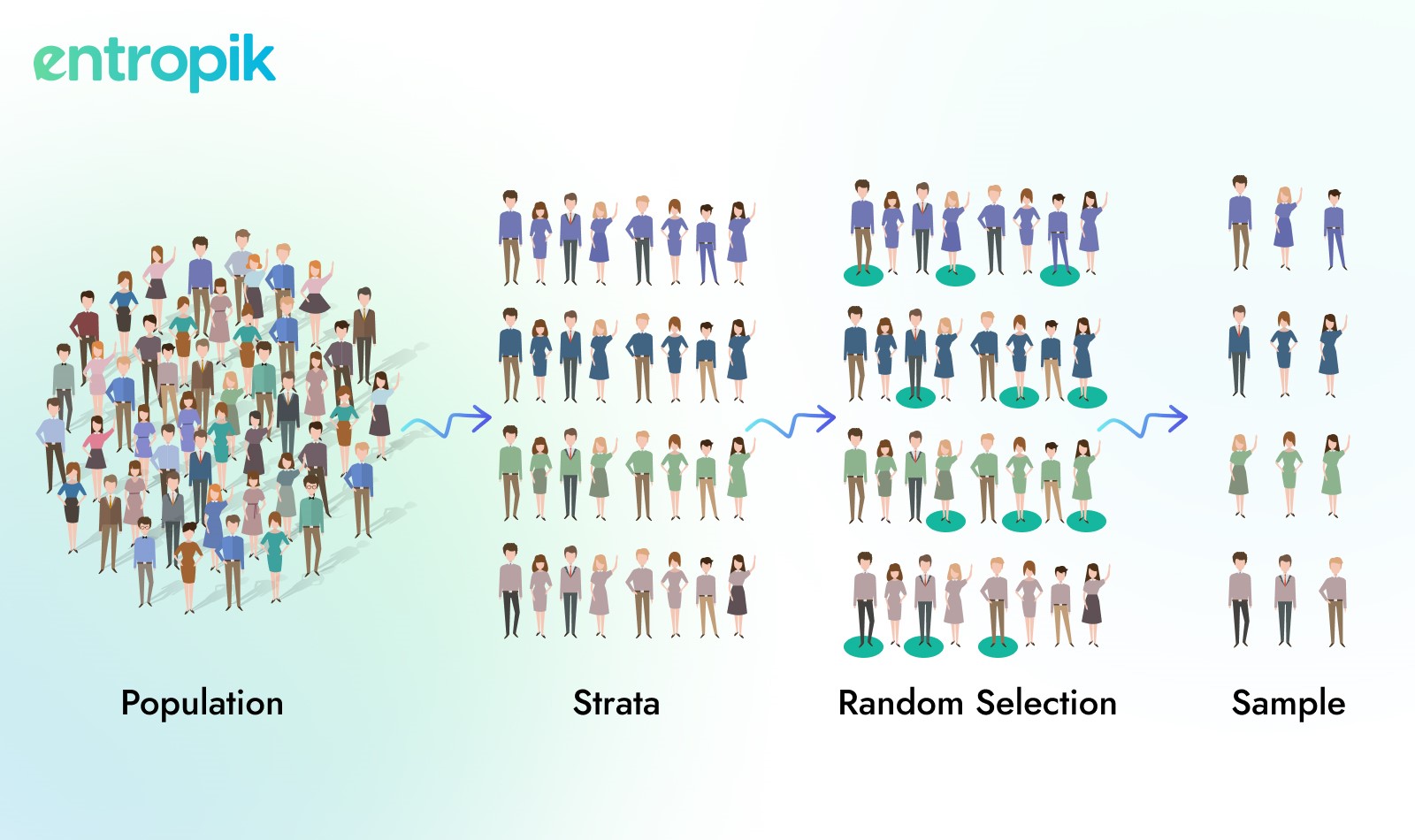
- Define the population: Identify the entire population you wish to study. The population must be large enough to divide into meaningful subgroups.
- Identify the strata: Subgroups or strata are created based on one or more characteristics. These could be based on demographics such as age, gender, education level, or geographic region. The key is that these subgroups must be mutually exclusive; every individual in the population should fit into only one stratum.
- Determine the sample size for each stratum: You need to decide how many individuals to sample from each stratum. This can be done using proportionate sampling (where the sample size in each stratum reflects its proportion in the population) or disproportionate sampling (where sample sizes differ from the population proportions).
- Randomly sample from each stratum: Once the strata and sample sizes are determined, you apply random sampling methods to select individuals from each subgroup. This can involve simple random sampling or systematic random sampling techniques.
- Combine the samples: Finally, once the random sampling is complete within each stratum, you combine the samples to create the final dataset, which represents the entire population.
Steps to Conduct Stratified Random Sampling
To further break down the process, here are the detailed steps for conducting stratified random sampling:
Step 1: Define Your Population and Strata
Start by identifying the entire population and the criteria for dividing them into subgroups. This could be any relevant characteristic, such as age, income, or geographic region.
Step 2: Separate the Population into Strata
Each member of the population should fit into one of the defined strata. For instance, if you are studying a population based on income levels, you could categorize them into “low income,” “middle income,” and “high income.”
Step 3: Determine the Sample Size for Each Stratum
Based on your research needs, you can either use proportionate stratified sampling, where the number of individuals sampled from each stratum reflects their proportion in the overall population, or disproportionate stratified sampling, where you deliberately choose different sample sizes for different strata.
Step4: Conduct Random Sampling Within Each Stratum
After determining the sample size, apply random sampling within each subgroup. This could involve using a random number generator or another method to ensure unbiased selection.
Step 5: Combine and Analyze the Data
Once the sampling is complete, combine the results from each stratum to analyze the data as a whole, ensuring each subgroup is proportionally represented.
Examples of Stratified Random Sampling
Example 1: Environmental Research
Scenario: An environmental scientist wants to study the level of pollution in a city’s air, which varies by region (e.g., urban, suburban, rural). The population of each region is different, and the pollution levels may vary significantly depending on the area.
Implementation: The researcher will stratify the population into these three regions and then randomly sample 2,500 from the urban group, 1,500 from the suburban group, and 1,000 from the rural group. This ensures that the air pollution data accurately represents all areas.
Example 2: Political Polling
Scenario: A polling organization is conducting a political survey in a country with diverse ethnic groups. The population consists of three major groups, and the polling needs to represent each group proportionally.
Implementation: Using stratified random sampling, the organization will select a proportional sample from each group—1,200 from Group A, 1,050 from Group B, and 750 from Group C. This ensures fair representation in the final survey results.
Example 3: Customer Feedback in Banking
Scenario: A bank wants to assess customer satisfaction with a new online banking platform. The bank has customers with varying account types (savings, checking, and credit). Each account type has a different number of users, so stratified random sampling can be used.
Implementation: The bank will randomly select 1,000 customers from savings accounts, 750 from checking, and 500 from credit card holders. This ensures that feedback is well-distributed among different user types.
Example 4: Agricultural Research
Scenario: A government agency wants to examine crop yields across different farming regions in a country. Since regions may have different climates and soil types, stratified random sampling is used to ensure accurate representation.
Implementation: The agency will select 3,000 farms from the North, 2,500 from the South, 2,000 from the East, and 1,500 from the West to ensure that differences in crop yields are reflected across all regions.
Example 5: Health Research
Scenario: A public health researcher is studying the effectiveness of a new diabetes drug. The city population of 100,000 people is diverse in terms of age, which may affect responses to the drug. Stratified random sampling can be applied across age groups to ensure adequate representation.
Implementation: The researcher would randomly select 500 participants from the 0-19 age group, 1,500 from 20-39, and so on, ensuring that each age group is properly represented.
When to Use Stratified Random Sampling
Stratified random sampling is ideal when you know that certain subgroups within your population have different characteristics or behaviors. Researchers use this method in the following scenarios:
- When there is significant diversity within the population: For example, a study on income inequality may need to represent different income groups proportionally.
- When accurate representation of subgroups is essential: If the goal is to ensure each subgroup within a population is represented, stratified sampling is crucial.
- When the researcher wants to reduce bias and improve precision: By sampling each stratum separately, the method ensures even small groups in the population are represented, reducing the risk of bias.
Why Researchers Use Stratified Random Sampling
Researchers choose stratified random sampling for several reasons:
Improved Accuracy: By ensuring that all relevant subgroups are included in the sample, this method leads to more accurate and generalizable results.
Reduced Bias: Since each subgroup is treated equally, there's less chance of over-representing certain characteristics while under-representing others.
Better Comparisons: If your goal is to compare behaviors or outcomes across different subgroups, stratified sampling makes it easy to do so.
Advantages of Stratified Random Sampling
- Ensures Representativeness: Stratified random sampling ensures that every subgroup is represented in the final sample, improving the accuracy and generalizability of the results.
- Increased Statistical Precision: By reducing the variability within each stratum, this method leads to more precise and reliable estimates.
- Flexible for Various Research Needs: It allows researchers to customize the sample sizes for each subgroup, depending on the research objectives.
- Better Comparability: Stratified sampling makes it easy to compare results across subgroups, as each group is equally represented.
Disadvantages of Stratified Random Sampling
- Complexity: Dividing the population into strata and then performing random sampling within each subgroup requires more effort and planning compared to simple random sampling.
- Difficulty in Stratum Identification: If the strata are not well-defined, it can lead to overlap or ambiguity, compromising the study’s results.
- Time-Consuming: Implementing stratified random sampling can be more time-consuming due to the need for detailed population data and complex random sampling techniques.
- Not Always Necessary: If the population is homogeneous, simple random sampling might be sufficient, making stratified sampling unnecessarily complicated.
Frequently Asked Questions (FAQs) About Stratified Random Sampling
Q1: How is stratified random sampling different from cluster sampling?
A: In stratified random sampling, the population is divided into strata based on specific characteristics, and random samples are taken from each stratum. In cluster sampling, the population is divided into clusters, and entire clusters are randomly selected for sampling.
Q2: When should I use stratified random sampling?
A: Use stratified random sampling when you want to ensure that all subgroups within a population are represented in your sample. It’s especially useful when subgroups have different characteristics that could affect the outcome of your study.
Q3: What is proportionate stratified sampling?
A: In proportionate stratified sampling, the size of the sample drawn from each stratum is proportional to the size of the stratum in the overall population. This ensures that larger groups have a bigger presence in the final sample.
Q4: Can stratified random sampling be used for qualitative research?
A: Yes, stratified random sampling can be used in qualitative research, particularly when the researcher wants to ensure diversity in the sample across specific characteristics.
Q5: What are common challenges in stratified random sampling?
A: Some challenges include accurately defining strata, ensuring random selection within each stratum, and obtaining detailed population data to effectively divide the population.
How Qatalyst Supports Stratified Random Sampling?
Qatalyst, an AI-powered user research platform from Entropik, simplifies and enhances the process of stratified random sampling for researchers and product managers. Here’s how it supports this methodology:
- Segmentation of Populations: Qatalyst allows researchers to easily define and create strata based on demographic, behavioral, or psychographic characteristics. Whether it’s dividing a population by age, income, or preferences, Qatalyst ensures that each subgroup is appropriately segmented for sampling.
- Automated Sampling: Qatalyst automates the process of continuing to support the stratified random sampling process:
- Advanced Data Collection: Qatalyst not only enables efficient sampling but also helps in collecting detailed consumer feedback. With tools such as facial coding and eye tracking, it ensures that even the most granular data is captured across different strata, making the insights more robust.
- Customizable Sampling Techniques: Whether you’re interested in proportionate or disproportionate stratified random sampling, Qatalyst provides the flexibility to adjust sample sizes according to your research objectives. This ensures that each subgroup is represented in the most relevant manner.
- Real-Time Insights: Qatalyst delivers real-time data analysis, helping researchers see how different subgroups respond to products, services, or campaigns. This makes it easier to compare responses across strata, aiding in better decision-making.
- Integration with Predictive AI: By leveraging predictive AI, Qatalyst helps forecast how each subgroup might behave in the future based on current and past behavior patterns. This is especially useful in longitudinal studies where tracking changes in specific subgroups over time is crucial.
Incorporating stratified random sampling into your research with the help of Qatalyst ensures that your data is both representative and actionable. It combines the power of AI-driven insights with rigorous sampling techniques to help you make better, data-backed decisions.
{{cta-button}}
Conclusion
In conclusion, stratified random sampling is a powerful method that offers a more nuanced and representative understanding of the population, especially in research where subgroup diversity plays a critical role. Despite its complexities, its benefits far outweigh its challenges, particularly when enhanced by platforms like Qatalyst. Whether you’re conducting academic research or marketing studies, using stratified random sampling ensures precision and accuracy, helping you derive meaningful insights that can drive your project forward.















.jpg)






















































































